机器学习已经越来越普及,渐渐的被应用到各行各业中。作为一个程序员,如何学习机器学习呢?在本系列文章中,我根据我学习的经验带大家了解一下机器学习的基础知识。
我原本是一名嵌入式开发工程师,2018年开始自学机器学习的知识,目前主要从事深度学习CV方向的工作。最初刚接触机器学习,我也是苦于如何入门。在搜索了很多资料后,找到了coursera上的Machine Learning课程,通过学习了完整的课程,最后掌握了机器学习的基础知识,为以后学习深度学习打下了基础。所以本系列文章,我将以Machine Learning课程和练习为基础,带大家了解什么是机器学习。今天我们先来了解一下线性回归。本篇文章是希望大家都能看懂,可以对线性回归有一个初步的了解,所以这里不会深入的做一些原理的推导。
1.线性回归简介
什么是线性回归呢?我们以房价的数据作为例子,来描述什么是线性回归。先看以下表格中的数据。
| 面积(㎡) | 价格(万元) |
|---|---|
| 210 | 460 |
| 141 | 232 |
| 153 | 315 |
| 85 | 178 |
| … | … |
观察上面的数据,同时结合日常生活的中的常识,我们可以得出一个结论,面积与价格之间存在的某种关系,但是目前这种关系是什么我们还不能确定,但我们可以先用公式表示它们的关系:
$H=θ_0 + xθ_1$ (1)
其中H为价格,x为面积。那么如果我们确定了$θ_0$和$θ_1$的值,就可以了确定了面积和价格之间的关系了。H和x都是表格中的数据是已知的,可以使用大量的数据来确定这个两个值,这样面积和价格之间就可以使用一个线性函数表示,那么确定这两个值的过程就称为线性回归。
我们也知道房价不仅仅和面积有关,还可能跟其他很多因素有关。观察下表,表中除了面积之外,又增加了几个其他特征。
| 面积(㎡) | 卧室数量 | 楼层 | 房龄 | 价格(万元) |
|---|---|---|---|---|
| 210 | 5 | 1 | 45 | 460 |
| 141 | 3 | 2 | 40 | 232 |
| 153 | 3 | 2 | 30 | 315 |
| 85 | 2 | 1 | 36 | 178 |
这时我们的公式1更新为以下公式:
$H=θ_0+x_1θ_1+x_2θ_2+ ……+x_nθ_n$ (2)
如果$θ_0$到$θ_n$的值初始化为随机值,那么通过公式2计算出的房价H与真实值一定会存在误差。如果调整参数$θ_0$到$θ_n$的值使H的值尽量解决真实的价格,那么是不是能确定面积和价格之间的关系,从而可以根据面积来预测房屋的大致价格。
2.损失函数
既然使用公式2计算出房价H与真实值存在一定的误差,那么我们首先需要用一个公式来描述这个误差,这个公式就叫做损失函数,用J来表示。定义如下:
$J(θ_0,θ_1,θ_1,……,θ_n)=\frac{1}{2m} \sum_{i=1}^m(h(x^{(i)})-y^{(i)})^2$ (3)
在上面公式3中,$θ$是需要求的未知变量,x与y是上面表格中的已知量,那么我们如何计算$θ$呢,这里我们就会用到机器学习里常用的一种方法梯度下降法。
3.梯度下降
梯度下降通过不断的迭代去更新$\theta$的值来降低损失函数的值,公式如下:
reapeat{
$\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1,…,\theta_n)$ (4)
}
公式4中$\alpha$代表着学习率,一般是0.1、0.01等这样小于1的实数,是需要根据实际情况进行调整的。
$\theta_j$代表着本次迭代需要更新的参数。$\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1,…,\theta_n)$这部分是J对$\theta_j$的偏导,求出来的值是当前$\theta_j$的梯度值,是一个向量,所以是有方向的。它的方向就是变化率最快的方向,也是该方向的最大值。通俗点说就是求当前$\theta_j$值对误差做出的贡献。所以可以通过迭代的方式用$\theta_j$减去学习率乘以$\theta_j$对误差做出的贡献更新参数$\theta_j$的值。更新后的$\theta_j$计算出的损失值会比原来小。通过若干次迭代,损失函数就会收敛到一个比较小的值,就可以停止迭代,这个过程也可称为训练。注意,这里只是简述了一下梯度下降的过程,也就是训练过程,在实际中还需考虑很多问题,比如局部最优解,过拟合和欠拟合等,不过这些问题都会有解决办法,后面的文章会讲到。
我举个简单的梯度下降的例子帮助大家理解一下。假设有简化一点的损失函数如下:
$J=\theta^2$ (5)
其实很容易可以看出这个是一个开口向上的抛物线,而且它只有一个最低点,也就是当$\theta$为0时,$J=0$。
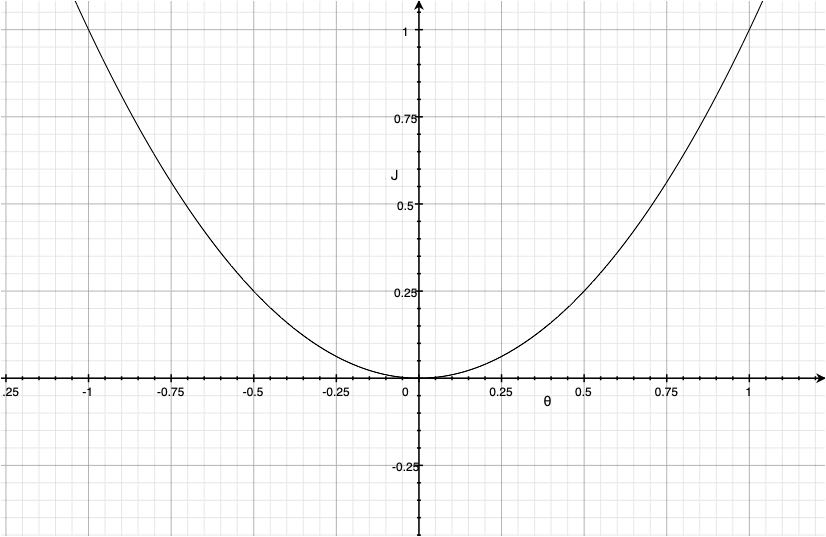
首先假设$\theta$的初始值为1。
$\theta^0=1$ 得出 $J=1$
然后做一次梯度下降的迭代,这里我们选择学习率$\alpha=0.4$。
$\theta^1 = \theta^0 -\alpha\frac{\partial}{\partial\theta^0}J$
$\theta^1=1-0.4\times2\theta^0=1-0.8=0.2$
$J=(\theta^1)^2 = 0.04$
使用更新后的$\theta^1$的值继续迭代。
$\theta^2 = \theta^1 -\alpha\frac{\partial}{\partial\theta^1}J$
$\theta^2=0.2-0.4\times2\theta^1=0.2-0.4\times0.4=0.04$
$J=(\theta^2)^2 = 0.0016$
$\theta^3 = \theta^2 -\alpha\frac{\partial}{\partial\theta^2}J$
$\theta^3=0.04-0.4\times2\theta^2=0.04-0.4\times0.08=0.008$
$J=(\theta^3)^2=6.4\times10^{-5}$
$\theta^4 = \theta^3 -\alpha\frac{\partial}{\partial\theta^3}J$
$\theta^4=0.008-0.4\times2\theta^3=0.008-0.4\times0.016=0.0016$
$J=(\theta^4)^2 = 2.56\times10^{-6}$
可以看到在第四次迭代的时候我们的损失函数$J$的值就已经很小了,如果继续迭代下去$J$的值会趋近于0。这时我们可以停止训练,得到了一个合适的参数$\theta=0.0016$,梯度下降的过程大致如下图。
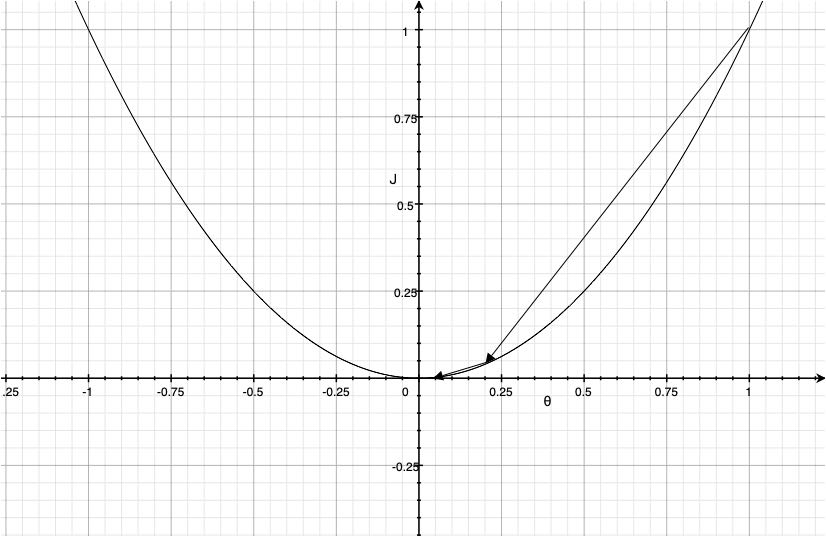
4.总结
我们从数据入手,简单描述了一下什么是线性回归。学习了一元线性回归的公式和多元线性回归公式。同时,利用线性回归的公式构造出一个损失函数的公式。损失函数是在训练过程中需要用到的,训练的前提是需要有大量的数据,这里以房价数据为例,我们可以通过梯度下降来计算$\theta$参数,来描述房屋特征值与房价直接的关系,这样就完成了线性回归的过程。